The Length-Constrained Brachistochrone#
Things you’ll learn through this example
How to connect the outputs from a trajectory to a downstream system.
This is a modified take on the brachistochrone problem. In this instance, we assume that the quantity of wire available is limited. Now, we seek to find the minimum time brachistochrone trajectory subject to a upper-limit on the arclength of the wire.
The most efficient way to approach this problem would be to treat the arc-length \(S\) as an integrated state variable. In this case, as is often the case in real-world MDO analyses, the implementation of our arc-length function is not integrated into our pseudospectral approach. Rather than rewrite an analysis tool to accommodate the pseudospectral approach, the arc-length analysis simply takes the result of the trajectory in its entirety and computes the arc-length constraint via the trapezoidal rule:\
(61)#\[\begin{align}
S &= \frac{1}{2} \left( \sum_{i=1}^{N-1} \sqrt{1 + \frac{1}{\tan{\theta_{i-1}}}} + \sqrt{1 + \frac{1}{\tan{\theta_{i}}}} \right) \left(x_{i-1} - x_i \right)
\end{align}\]
The OpenMDAO component used to compute the arclength is defined as follows:
import numpy as np
from openmdao.api import ExplicitComponent
class ArcLengthComp(ExplicitComponent):
def initialize(self):
self.options.declare('num_nodes', types=(int,))
def setup(self):
nn = self.options['num_nodes']
self.add_input('x', val=np.ones(nn), units='m', desc='x at points along the trajectory')
self.add_input('theta', val=np.ones(nn), units='rad',
desc='wire angle with vertical along the trajectory')
self.add_output('S', val=1.0, units='m', desc='arclength of wire')
self.declare_partials(of='S', wrt='*', method='cs')
def compute(self, inputs, outputs, discrete_inputs=None, discrete_outputs=None):
x = inputs['x']
theta = inputs['theta']
dy_dx = -1.0 / np.tan(theta)
dx = np.diff(x)
f = np.sqrt(1 + dy_dx**2)
# trapezoidal rule
fxm1 = f[:-1]
fx = f[1:]
outputs['S'] = 0.5 * np.dot(fxm1 + fx, dx)
Note
In this example, the number of nodes used to compute the arclength is needed when building the problem.
The transcription object is initialized and its attribute grid_data.num_nodes is used to provide the number of total nodes (the number of points in the timeseries) to the downstream arc length calculation.
Show code cell outputs
import numpy as np
import openmdao.api as om
class BrachistochroneODE(om.ExplicitComponent):
def initialize(self):
self.options.declare('num_nodes', types=int)
self.options.declare('static_gravity', types=(bool,), default=False,
desc='If True, treat gravity as a static (scalar) input, rather than '
'having different values at each node.')
def setup(self):
nn = self.options['num_nodes']
# Inputs
self.add_input('v', val=np.zeros(nn), desc='velocity', units='m/s')
if self.options['static_gravity']:
self.add_input('g', val=9.80665, desc='grav. acceleration', units='m/s/s',
tags=['dymos.static_target'])
else:
self.add_input('g', val=9.80665 * np.ones(nn), desc='grav. acceleration', units='m/s/s')
self.add_input('theta', val=np.ones(nn), desc='angle of wire', units='rad')
self.add_output('xdot', val=np.zeros(nn), desc='velocity component in x', units='m/s',
tags=['dymos.state_rate_source:x', 'dymos.state_units:m'])
self.add_output('ydot', val=np.zeros(nn), desc='velocity component in y', units='m/s',
tags=['dymos.state_rate_source:y', 'dymos.state_units:m'])
self.add_output('vdot', val=np.zeros(nn), desc='acceleration magnitude', units='m/s**2',
tags=['dymos.state_rate_source:v', 'dymos.state_units:m/s'])
self.add_output('check', val=np.zeros(nn), desc='check solution: v/sin(theta) = constant',
units='m/s')
# Setup partials
arange = np.arange(self.options['num_nodes'])
self.declare_partials(of='vdot', wrt='theta', rows=arange, cols=arange)
self.declare_partials(of='xdot', wrt='v', rows=arange, cols=arange)
self.declare_partials(of='xdot', wrt='theta', rows=arange, cols=arange)
self.declare_partials(of='ydot', wrt='v', rows=arange, cols=arange)
self.declare_partials(of='ydot', wrt='theta', rows=arange, cols=arange)
self.declare_partials(of='check', wrt='v', rows=arange, cols=arange)
self.declare_partials(of='check', wrt='theta', rows=arange, cols=arange)
if self.options['static_gravity']:
c = np.zeros(self.options['num_nodes'])
self.declare_partials(of='vdot', wrt='g', rows=arange, cols=c)
else:
self.declare_partials(of='vdot', wrt='g', rows=arange, cols=arange)
def compute(self, inputs, outputs):
theta = inputs['theta']
cos_theta = np.cos(theta)
sin_theta = np.sin(theta)
g = inputs['g']
v = inputs['v']
outputs['vdot'] = g * cos_theta
outputs['xdot'] = v * sin_theta
outputs['ydot'] = -v * cos_theta
outputs['check'] = v / sin_theta
def compute_partials(self, inputs, partials):
theta = inputs['theta']
cos_theta = np.cos(theta)
sin_theta = np.sin(theta)
g = inputs['g']
v = inputs['v']
partials['vdot', 'g'] = cos_theta
partials['vdot', 'theta'] = -g * sin_theta
partials['xdot', 'v'] = sin_theta
partials['xdot', 'theta'] = v * cos_theta
partials['ydot', 'v'] = -cos_theta
partials['ydot', 'theta'] = v * sin_theta
partials['check', 'v'] = 1 / sin_theta
partials['check', 'theta'] = -v * cos_theta / sin_theta ** 2
import openmdao.api as om
import dymos as dm
import matplotlib.pyplot as plt
from dymos.examples.brachistochrone.brachistochrone_ode import BrachistochroneODE
MAX_ARCLENGTH = 11.9
OPTIMIZER = 'SLSQP'
p = om.Problem(model=om.Group())
p.add_recorder(om.SqliteRecorder('length_constrained_brach_sol.db'))
if OPTIMIZER == 'SNOPT':
p.driver = om.pyOptSparseDriver()
p.driver.options['optimizer'] = OPTIMIZER
p.driver.opt_settings['Major iterations limit'] = 1000
p.driver.opt_settings['Major feasibility tolerance'] = 1.0E-6
p.driver.opt_settings['Major optimality tolerance'] = 1.0E-5
p.driver.opt_settings['iSumm'] = 6
p.driver.opt_settings['Verify level'] = 3
else:
p.driver = om.ScipyOptimizeDriver()
p.driver.declare_coloring()
# Create the transcription so we can get the number of nodes for the downstream analysis
tx = dm.Radau(num_segments=20, order=3, compressed=False)
traj = dm.Trajectory()
phase = dm.Phase(transcription=tx, ode_class=BrachistochroneODE)
traj.add_phase('phase0', phase)
p.model.add_subsystem('traj', traj)
phase.set_time_options(fix_initial=True, duration_bounds=(.5, 10))
phase.add_state('x', units='m', rate_source='xdot', fix_initial=True, fix_final=True)
phase.add_state('y', units='m', rate_source='ydot', fix_initial=True, fix_final=True)
phase.add_state('v', units='m/s', rate_source='vdot', fix_initial=True, fix_final=False)
phase.add_control('theta', units='deg', lower=0.01, upper=179.9,
continuity=True, rate_continuity=True)
phase.add_parameter('g', units='m/s**2', opt=False, val=9.80665)
# Minimize time at the end of the phase
phase.add_objective('time', loc='final', scaler=1)
# p.model.options['assembled_jac_type'] = top_level_jacobian.lower()
# p.model.linear_solver = DirectSolver(assemble_jac=True)
# Add the arc length component
p.model.add_subsystem('arc_length_comp',
subsys=ArcLengthComp(num_nodes=tx.grid_data.num_nodes))
p.model.connect('traj.phase0.timeseries.theta', 'arc_length_comp.theta')
p.model.connect('traj.phase0.timeseries.x', 'arc_length_comp.x')
p.model.add_constraint('arc_length_comp.S', upper=MAX_ARCLENGTH, ref=1)
p.setup(check=True)
phase.set_time_val(initial=0.0, duration=2.0)
phase.set_state_val('x', [0, 10])
phase.set_state_val('y', [10, 5])
phase.set_state_val('v', [0, 9.9])
phase.set_control_val('theta', [5, 100])
phase.set_parameter_val('g', 9.80665)
p.run_driver()
p.record(case_name='final')
# Generate the explicitly simulated trajectory
exp_out = traj.simulate()
# Extract the timeseries from the implicit solution and the explicit simulation
x = p.get_val('traj.phase0.timeseries.x')
y = p.get_val('traj.phase0.timeseries.y')
t = p.get_val('traj.phase0.timeseries.time')
theta = p.get_val('traj.phase0.timeseries.theta')
x_exp = exp_out.get_val('traj.phase0.timeseries.x')
y_exp = exp_out.get_val('traj.phase0.timeseries.y')
t_exp = exp_out.get_val('traj.phase0.timeseries.time')
theta_exp = exp_out.get_val('traj.phase0.timeseries.theta')
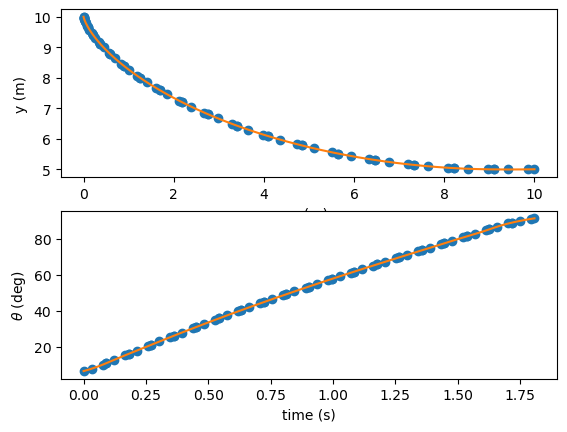
fig, axes = plt.subplots(nrows=2, ncols=1)
axes[0].plot(x, y, 'o')
axes[0].plot(x_exp, y_exp, '-')
axes[0].set_xlabel('x (m)')
axes[0].set_ylabel('y (m)')
axes[1].plot(t, theta, 'o')
axes[1].plot(t_exp, theta_exp, '-')
axes[1].set_xlabel('time (s)')
axes[1].set_ylabel(r'$\theta$ (deg)')
plt.show()
--- Constraint Report [traj] ---
--- phase0 ---
None
INFO: checking out_of_order
INFO: checking system
INFO: checking solvers
INFO: checking dup_inputs
INFO: checking missing_recorders
INFO: checking unserializable_options
INFO: checking comp_has_no_outputs
INFO: checking auto_ivc_warnings
Full total jacobian for problem 'problem' was computed 3 times, taking 0.38079927500007216 seconds.
Total jacobian shape: (220, 296)
Jacobian shape: (220, 296) (2.35% nonzero)
FWD solves: 1 REV solves: 11
Total colors vs. total size: 12 vs 220 (94.55% improvement)
Sparsity computed using tolerance: 1e-25
Time to compute sparsity: 0.3808 sec
Time to compute coloring: 0.1805 sec
Memory to compute coloring: 0.3750 MB
Coloring created on: 2024-12-11 19:23:49
Optimization terminated successfully (Exit mode 0)
Current function value: 1.8085985207863569
Iterations: 5
Function evaluations: 5
Gradient evaluations: 5
Optimization Complete
-----------------------------------
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/visualization/opt_report/opt_report.py:625: UserWarning: Attempting to set identical low and high ylims makes transformation singular; automatically expanding.
ax.set_ylim([ymin_plot, ymax_plot])
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/group.py:1137: DerivativesWarning:Constraints or objectives [ode_eval.control_interp.control_rates:theta_rate, ode_eval.control_interp.control_rates:theta_rate2, ode_eval.control_interp.control_values:theta] cannot be impacted by the design variables of the problem because no partials were defined for them in their parent component(s).
Simulating trajectory traj
Done simulating trajectory traj
