The Brachistochrone with externally-sourced initial state values

Contents

The Brachistochrone with externally-sourced initial state values#

Things you’ll learn through this example

How to link phase initial time and duration.

This is another modification of the brachistochrone in which the target initial time and duration of a phase is provided by an external source (an IndepVarComp in this case).

Rather than the external value being directly connected to the phase, the values are “linked” via state_ivc’s t_initial and t_duration.

The following script fully defines the brachistochrone problem with Dymos and solves it. A new IndepVarComp is added before the trajectory which provides t_initial and t_duration. These two outputs are connected directly into the phase. Also, it’s important to set input_duration and input_initial to True inside of set_time_options

import openmdao.api as om
import dymos as dm
import matplotlib.pyplot as plt
from dymos.examples.brachistochrone.brachistochrone_ode import BrachistochroneODE
#
# Define the OpenMDAO problem
#
p = om.Problem(model=om.Group())

# Instantiate the transcription so we can get the number of nodes from it while
# building the problem.
tx = dm.GaussLobatto(num_segments=10, order=3)

# Add an indep var comp to provide the external control values
ivc = p.model.add_subsystem('states_ivc', om.IndepVarComp(), promotes_outputs=['*'])

# Add the output to provide the values of theta at the control input nodes of the transcription.
# ivc.add_output('x0', shape=(1,), units='m')
ivc.add_output('t_initial', val=0.0, units='s')
ivc.add_output('t_duration', val=10., units='s')
ivc.add_design_var('t_duration', units='s', lower=0.1, upper=10.)

# Connect x0 to the state error component so we can constrain the given value of x0
# to be equal to the value chosen in the phase.
# p.model.connect('x0', 'state_error_comp.x0_target')
# p.model.connect('traj.phase0.timeseries.x', 'state_error_comp.x0_actual',
#                 src_indices=[0])
p.model.connect('t_initial', 'traj.phase0.t_initial')
p.model.connect('t_duration', 'traj.phase0.t_duration')
#
# Define a Trajectory object
#
traj = dm.Trajectory()
p.model.add_subsystem('traj', subsys=traj)

#
# Define a Dymos Phase object with GaussLobatto Transcription
#
phase = dm.Phase(ode_class=BrachistochroneODE,
                 transcription=tx)
traj.add_phase(name='phase0', phase=phase)

#
# Set the time options
# Time has no targets in our ODE.
# We fix the initial time so that the it is not a design variable in the optimization.
# The duration of the phase is allowed to be optimized, but is bounded on [0.5, 10]
# which is set above in state_ivc
phase.set_time_options(input_duration=True, input_initial=True, units='s')

#
# Set the time options
# Initial values of positions and velocity are all fixed.
# The final value of position are fixed, but the final velocity is a free variable.
# The equations of motion are not functions of position, so 'x' and 'y' have no targets.
# The rate source points to the output in the ODE which provides the time derivative of the
# given state.
phase.add_state('x', fix_initial=True, fix_final=True, units='m', rate_source='xdot')
phase.add_state('y', fix_initial=True, fix_final=True, units='m', rate_source='ydot')
phase.add_state('v', fix_initial=True, fix_final=False, units='m/s',
                rate_source='vdot', targets=['v'])

# Define theta as a control.
# Use opt=False to allow it to be connected to an external source.
# Arguments lower and upper are no longer valid for an input control.
phase.add_control(name='theta', units='rad', targets=['theta'])
# Minimize final time.
phase.add_objective('time', loc='final')

# Set the driver.
p.driver = om.ScipyOptimizeDriver()

# Allow OpenMDAO to automatically determine our sparsity pattern.
# Doing so can significant speed up the execution of Dymos.
p.driver.declare_coloring()

# Setup the problem
p.setup(check=True)

# Now that the OpenMDAO problem is setup, we can set the values of the states.
# p.set_val('x0', 0.0, units='m')
# Here we're intentially setting the intiial x value to something other than zero, just
# to demonstrate that the optimizer brings it back in line with the value of x0 set above.
phase.set_state_val('x', [0, 10],
                    units='m')

phase.set_state_val('y', [10, 5],
                    units='m')

phase.set_state_val('v', [0, 9.9],
                    units='m/s')

phase.set_control_val('theta', [5, 100.5],
                      units='deg')

# Run the driver to solve the problem
dm.run_problem(p, simulate=True)

--- Constraint Report [traj] ---
    --- phase0 ---
        None

INFO: checking out_of_order...

INFO:     out_of_order check complete (0.000371 sec).

INFO: checking system...

INFO:     system check complete (0.000024 sec).

INFO: checking solvers...

INFO:     solvers check complete (0.000303 sec).

INFO: checking dup_inputs...

INFO:     dup_inputs check complete (0.000098 sec).

INFO: checking missing_recorders...

INFO:     missing_recorders check complete (0.000002 sec).

INFO: checking unserializable_options...

INFO:     unserializable_options check complete (0.003207 sec).

INFO: checking comp_has_no_outputs...

INFO:     comp_has_no_outputs check complete (0.000060 sec).

INFO: checking auto_ivc_warnings...

INFO:     auto_ivc_warnings check complete (0.000003 sec).

INFO: checking out_of_order...

INFO:     out_of_order check complete (0.000239 sec).

INFO: checking system...

INFO:     system check complete (0.000017 sec).

INFO: checking solvers...

INFO:     solvers check complete (0.000149 sec).

INFO: checking dup_inputs...

INFO:     dup_inputs check complete (0.000069 sec).

INFO: checking missing_recorders...

INFO:     missing_recorders check complete (0.000002 sec).

INFO: checking unserializable_options...

INFO:     unserializable_options check complete (0.003332 sec).

INFO: checking comp_has_no_outputs...

INFO:     comp_has_no_outputs check complete (0.000050 sec).

INFO: checking auto_ivc_warnings...

INFO:     auto_ivc_warnings check complete (0.000002 sec).

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/recorders/sqlite_recorder.py:230: UserWarning:The existing case recorder file, /home/runner/work/dymos/dymos/docs/dymos_book/examples/brachistochrone/problem_out/dymos_solution.db, is being overwritten.

Full total jacobian for problem 'problem' was computed 3 times, taking 0.07906755399994836 seconds.
Total jacobian shape: (40, 50) 


Jacobian shape: (40, 50)  (13.40% nonzero)
FWD solves: 8   REV solves: 0
Total colors vs. total size: 8 vs 50  (84.00% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.0791 sec
Time to compute coloring:   0.0421 sec
Memory to compute coloring:   0.2500 MB
Coloring created on: 2025-01-15 21:09:46

Optimization terminated successfully    (Exit mode 0)
            Current function value: 1.8016052392021373
            Iterations: 39
            Function evaluations: 40
            Gradient evaluations: 39
Optimization Complete
-----------------------------------

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/group.py:1166: DerivativesWarning:Constraints or objectives [ode_eval.control_interp.control_rates:theta_rate, ode_eval.control_interp.control_rates:theta_rate2, ode_eval.control_interp.control_values:theta] cannot be impacted by the design variables of the problem because no partials were defined for them in their parent component(s).

Simulating trajectory traj

Done simulating trajectory traj

Problem: problem
Driver:  ScipyOptimizeDriver
  success     : True
  iterations  : 41
  runtime     : 7.0921E-01 s
  model_evals : 41
  model_time  : 2.6872E-02 s
  deriv_evals : 39
  deriv_time  : 2.0280E-01 s
  exit_status : SUCCESS

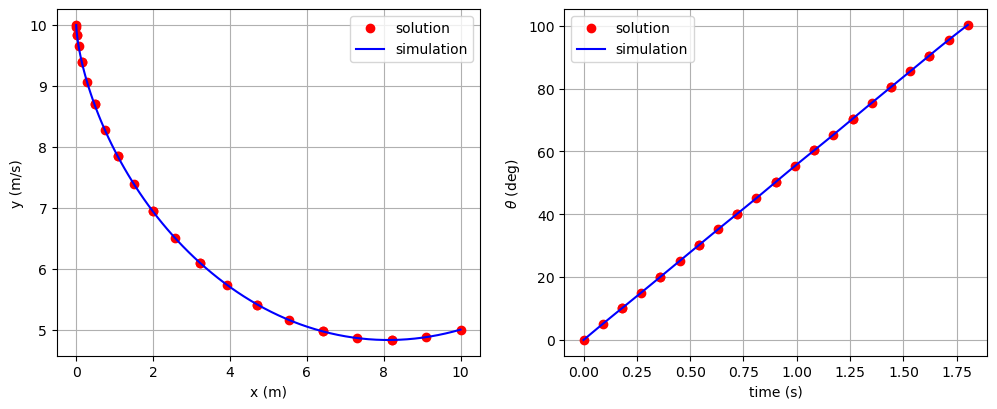
Plotting the results#

In the following cell, we load the solution and simulated results from their respective recorder files and plot the solution.

# Check the validity of our results.
sol = om.CaseReader(p.get_outputs_dir() / 'dymos_solution.db').get_case('final')
sim = om.CaseReader(traj.sim_prob.get_outputs_dir() / 'dymos_simulation.db').get_case('final')

# Plot the results
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12, 4.5))
axes[0].plot(sol.get_val('traj.phase0.timeseries.x'),
             sol.get_val('traj.phase0.timeseries.y'),
             'ro', label='solution')
axes[0].plot(sim.get_val('traj.phase0.timeseries.x'),
             sim.get_val('traj.phase0.timeseries.y'),
             'b-', label='simulation')
axes[0].set_xlabel('x (m)')
axes[0].set_ylabel('y (m/s)')
axes[0].legend()
axes[0].grid()
axes[1].plot(sol.get_val('traj.phase0.timeseries.time'),
             sol.get_val('traj.phase0.timeseries.theta', units='deg'),
             'ro', label='solution')
axes[1].plot(sim.get_val('traj.phase0.timeseries.time'),
             sim.get_val('traj.phase0.timeseries.theta', units='deg'),
             'b-', label='simulation')
axes[1].set_xlabel('time (s)')
axes[1].set_ylabel(r'$\theta$ (deg)')
axes[1].legend()
axes[1].grid()
plt.show()

../../_images/c53870a04a7923c575b8bfcae72c070e8fedaefb3667bbb4da952c4b071d9bb6.png