How can I more efficiently use finite-differenced components in the ODE?

Sometimes it’s overly burdensome to get the analytic partials for a component. In this case, OpenMDAO can use finite-differencing to approximate the partials of that component and then use those approximated partials when assembling the total derivatives. However, if a dense sub-jacobian pattern is prescribed somewhere within the ODE, it will effect all dependent calculations and cause related total jacobians to have dense patterns. In effect, a dense partial-derivative jacobian destroys the sparsity pattern of the problem. To alleviate this, OpenMDAO provides a mechanism to color the partials of a single component.

As an example, consider the minimum time-to-climb problem. The ODE of this problem consists of several components. In this case, we’re going to switch one of these components from using analytic derivatives to a finite-difference approximation. Here we use an option on the component so that we can toggle the use of partial coloring on and off for testing, but that’s not generally necessary.

class DynamicPressureCompFD(om.ExplicitComponent):
    def initialize(self):
        self.options.declare('num_nodes', types=int)
        self.options.declare('partial_coloring', types=bool, default=False)

    def setup(self):
        nn = self.options['num_nodes']

        self.add_input(name='rho', shape=(nn,), desc='atmospheric density', units='kg/m**3')
        self.add_input(name='v', shape=(nn,), desc='air-relative velocity', units='m/s')

        self.add_output(name='q', shape=(nn,), desc='dynamic pressure', units='N/m**2')

        self.declare_partials(of='q', wrt='rho', method='fd')
        self.declare_partials(of='q', wrt='v', method='fd')

        if self.options['partial_coloring']:
            self.declare_coloring(wrt=['*'], method='cs', tol=1.0E-6, num_full_jacs=2,
                                  show_summary=True, show_sparsity=False, min_improve_pct=10.)

    def compute(self, inputs, outputs):
        outputs['q'] = 0.5 * inputs['rho'] * inputs['v'] ** 2

Note

When using finite-differenced partials, they should not be specified in the compute_partials method. In fact, if all partials in the component are being approximated, compute_partials should just be omitted.

In this usage of declare_coloring, we use the following arguments:

• wrt=['*'] This is used to specify that we wish to find sparse partials with respect to all inputs.

• method=['fd'] We’re using finite differencing to approximate the partials for coloring. Using 'cs' here (complex-step) will result in more accurate derivatives if the model supports the use of complex inputs.

• tol=1.0E-6 Any value in the Jacobian with a value greater than this will be considered a non-zero. Since finite differencing is used and it generally encounters noise on the order of 1.0E-8, this tolerance should be larger than that. If using complex-step for the approximation method this tolerance can be smaller - as small as about 1.0E-15.

• num_full_jacs Compute the full jacobian this number of times before determining the partial sparsity pattern.

• min_improve_pct If the number of solves required to compute the derivatives isn’t reduced by at least this amount, then coloring is ignored and the dense jacobian is used.

• show_summary = True Print the sparsity of the partial derivative jacobian. This will display something like:

Jacobian shape: (60, 120)  ( 1.67% nonzero)
FWD solves: 2   REV solves: 0
Total colors vs. total size: 2 vs 120  (98.3% improvement)

Sparsity computed using tolerance: 1e-06
Time to compute sparsity: 0.011868 sec.
Time to compute coloring: 0.001385 sec.

• show_sparsity=True Display the sparsity pattern in standard output to provide a visual indication whether or not it is working. Here, this outputs the jacobian of rho with two diagonal bands - one for each of the two inputs.

Approx coloring for 'traj.phases.phase0.rhs_col.aero.q_comp' (class DynamicPressureCompFD)
f.............................f............................. 0  q
.f.............................f............................ 1  q
..f.............................f........................... 2  q
...f.............................f.......................... 3  q
....f.............................f......................... 4  q
.....f.............................f........................ 5  q
......f.............................f....................... 6  q
.......f.............................f...................... 7  q
........f.............................f..................... 8  q
.........f.............................f.................... 9  q
..........f.............................f................... 10  q
...........f.............................f.................. 11  q
............f.............................f................. 12  q
.............f.............................f................ 13  q
..............f.............................f............... 14  q
...............f.............................f.............. 15  q
................f.............................f............. 16  q
.................f.............................f............ 17  q
..................f.............................f........... 18  q
...................f.............................f.......... 19  q
....................f.............................f......... 20  q
.....................f.............................f........ 21  q
......................f.............................f....... 22  q
.......................f.............................f...... 23  q
........................f.............................f..... 24  q
.........................f.............................f.... 25  q
..........................f.............................f... 26  q
...........................f.............................f.. 27  q
............................f.............................f. 28  q
.............................f.............................f 29  q
|rho
                              |v

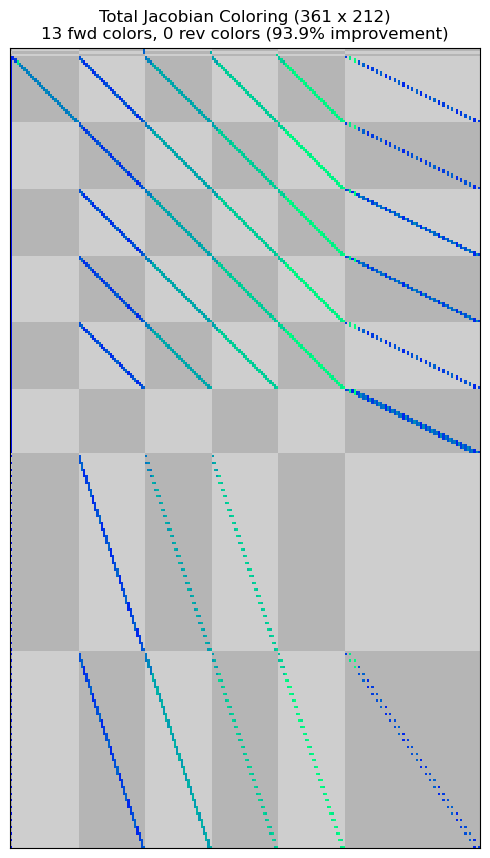
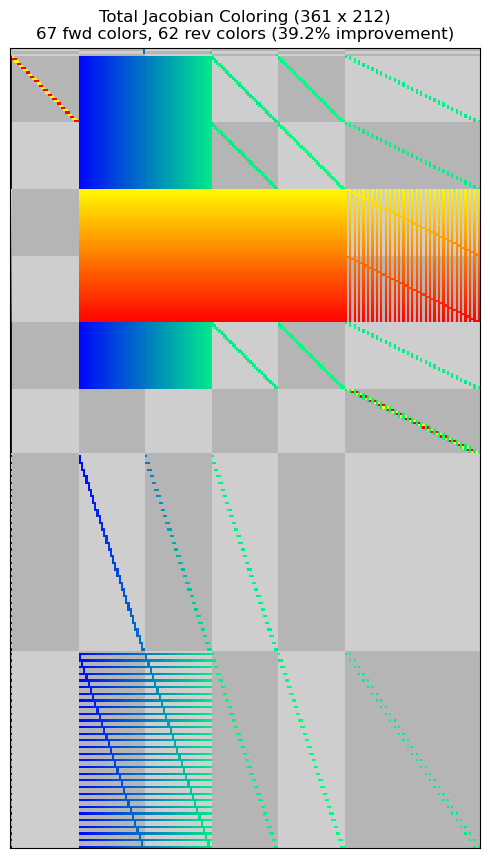
The sparsity patterns of the resulting total-derivative jacobian matrices are shown below. Finite differencing without partial derivative coloring causes the sparsity pattern to be dense for a large portion of the matrix. Since the dynamic pressure affects all of the defect constraints, the algorithm treats each defect constraint as if it is potentially dependent upon all altitude and velocity values throughout the phase. However, if partial derivative coloring is used, OpenMDAO recovers the same sparsity pattern as seen in the analytic derivative case.

Show code cell outputs Hide code cell outputs

class MinTimeClimbODE(om.Group):

    def initialize(self):
        self.options.declare('num_nodes', types=int)
        self.options.declare('fd', types=bool, default=False, desc='If True, use fd for partials')
        self.options.declare('partial_coloring', types=bool, default=False,
                             desc='If True and fd is True, color the approximated partials')

    def setup(self):
        nn = self.options['num_nodes']

        self.add_subsystem(name='atmos',
                           subsys=USatm1976Comp(num_nodes=nn),
                           promotes_inputs=['h'])

        self.add_subsystem(name='aero',
                           subsys=AeroGroup(num_nodes=nn,
                                            fd=self.options['fd'],
                                            partial_coloring=self.options['partial_coloring']),
                           promotes_inputs=['v', 'alpha', 'S'])

        self.connect('atmos.sos', 'aero.sos')
        self.connect('atmos.rho', 'aero.rho')

        self.add_subsystem(name='prop',
                           subsys=PropGroup(num_nodes=nn),
                           promotes_inputs=['h', 'Isp', 'throttle'])

        self.connect('aero.mach', 'prop.mach')

        self.add_subsystem(name='flight_dynamics',
                           subsys=FlightPathEOM2D(num_nodes=nn),
                           promotes_inputs=['m', 'v', 'gam', 'alpha'])

        self.connect('aero.f_drag', 'flight_dynamics.D')
        self.connect('aero.f_lift', 'flight_dynamics.L')
        self.connect('prop.thrust', 'flight_dynamics.T')

import os 
import matplotlib.pyplot as plt
import shutil

import openmdao.api as om

import dymos as dm
from dymos.examples.min_time_climb.doc.min_time_climb_ode_partial_coloring import MinTimeClimbODE


for fd in (False, True):
    if fd:
        pc_options = (False, True)
    else:
        pc_options = (False,)
    for pc in pc_options:
        header = 'Finite differenced component' if fd else 'Analytic derivatives in component'
        header += ' with partial coloring' if pc else ''

        #
        # Instantiate the problem and configure the optimization driver
        #
        p = om.Problem(model=om.Group())

        p.driver = om.pyOptSparseDriver()
        p.driver.options['optimizer'] = 'IPOPT'
        p.driver.options['print_results'] = False

        p.driver.opt_settings['max_iter'] = 500
        p.driver.opt_settings['print_level'] = 0
        p.driver.opt_settings['nlp_scaling_method'] = 'gradient-based'
        p.driver.opt_settings['tol'] = 1.0E-6
        p.driver.opt_settings['mu_strategy'] = 'adaptive'
        p.driver.opt_settings['bound_mult_init_method'] = 'mu-based'
        p.driver.opt_settings['mu_init'] = 0.01

        p.driver.declare_coloring(tol=1.0E-12)

        #
        # Instantiate the trajectory and phase
        #
        traj = dm.Trajectory()

        phase = dm.Phase(ode_class=MinTimeClimbODE,
                         ode_init_kwargs={'fd': fd, 'partial_coloring': pc},
                         transcription=dm.GaussLobatto(num_segments=30))

        traj.add_phase('phase0', phase)

        p.model.add_subsystem('traj', traj)

        #
        # Set the options on the optimization variables
        #
        phase.set_time_options(fix_initial=True, duration_bounds=(50, 400),
                               duration_ref=100.0)

        phase.add_state('r', fix_initial=True, lower=0, upper=1.0E6,
                        ref=1.0E3, defect_ref=1.0E3, units='m',
                        rate_source='flight_dynamics.r_dot')

        phase.add_state('h', fix_initial=True, lower=0, upper=20000.0,
                        ref=1.0E2, defect_ref=1.0E2, units='m',
                        rate_source='flight_dynamics.h_dot')

        phase.add_state('v', fix_initial=True, lower=10.0,
                        ref=1.0E2, defect_ref=1.0E2, units='m/s',
                        rate_source='flight_dynamics.v_dot')

        phase.add_state('gam', fix_initial=True, lower=-1.5, upper=1.5,
                        ref=1.0, defect_ref=1.0, units='rad',
                        rate_source='flight_dynamics.gam_dot')

        phase.add_state('m', fix_initial=True, lower=10.0, upper=1.0E5,
                        ref=1.0E3, defect_ref=1.0E3, units='kg',
                        rate_source='prop.m_dot')

        phase.add_control('alpha', units='deg', lower=-8.0, upper=8.0, scaler=1.0,
                          rate_continuity=True, rate_continuity_scaler=100.0,
                          rate2_continuity=False, targets=['alpha'])

        phase.add_parameter('S', val=49.2386, units='m**2', opt=False, targets=['S'])
        phase.add_parameter('Isp', val=1600.0, units='s', opt=False, targets=['Isp'])
        phase.add_parameter('throttle', val=1.0, opt=False, targets=['throttle'])

        #
        # Setup the boundary and path constraints
        #
        phase.add_boundary_constraint('h', loc='final', equals=20000, scaler=1.0E-3)
        phase.add_boundary_constraint('aero.mach', loc='final', equals=1.0)
        phase.add_boundary_constraint('gam', loc='final', equals=0.0)

        phase.add_path_constraint(name='h', lower=100.0, upper=20000, ref=20000)
        phase.add_path_constraint(name='aero.mach', lower=0.1, upper=1.8)

        # Minimize time at the end of the phase
        phase.add_objective('time', loc='final', ref=100.0)

        p.model.options['assembled_jac_type'] = 'csc'
        p.model.linear_solver = om.DirectSolver(assemble_jac=True)

        #
        # Setup the problem and set the initial guess
        #
        p.setup()

        p['traj.phase0.t_initial'] = 0.0
        p['traj.phase0.t_duration'] = 400

        p['traj.phase0.states:r'] = phase.interp('r', [0.0, 50000.0])
        p['traj.phase0.states:h'] = phase.interp('h', [100.0, 20000.0])
        p['traj.phase0.states:v'] = phase.interp('v', [135.964, 283.159])
        p['traj.phase0.states:gam'] = phase.interp('gam', [0.0, 0.0])
        p['traj.phase0.states:m'] = phase.interp('m', [19030.468, 10000.])
        p['traj.phase0.controls:alpha'] = phase.interp('alpha', [0.0, 0.0])

        #
        # Solve for the optimal trajectory
        #

        print(80 * '-')
        print(f'{"--- " + header + " ":-<80}')
        print(80 * '-', '\n')
        dm.run_problem(p)

        #
        # This code is intended to save the coloring plots for the documentation.
        # In practice, use the command line interface to view these files instead:
        # `openmdao view_coloring coloring_files/total_coloring.pkl --view`
        #
        from openmdao import __version__ as om_version
        om_version_tup = tuple((int(s) for s in om_version.split('-')[0].split('.')))

        # Handle the output directory behavior change as of OpenMAO 3.34.3-dev
        stfd = '_fd' if fd else ''
        stpc = '_pc' if pc else ''
        if om_version_tup > (3, 34, 2):
            saved_coloring_dir = f'coloring_files{stfd}{stpc}'
            if os.path.exists(saved_coloring_dir):
                shutil.rmtree(saved_coloring_dir)
            shutil.move(p.get_coloring_dir(mode='output'), saved_coloring_dir)
            _view_coloring(os.path.join(saved_coloring_dir, 'total_coloring.pkl'))
        else:
            coloring_dir = f'coloring_files{stfd}{stpc}'
            if fd or pc:
                if os.path.exists(coloring_dir):
                    shutil.rmtree(coloring_dir)
                shutil.move('coloring_files', coloring_dir)
            _view_coloring(os.path.join(coloring_dir, 'total_coloring.pkl'))

--- Constraint Report [traj] ---
    --- phase0 ---
        [final]   2.0000e+04 == h [m]
        [final]   1.0000e+00 == aero.mach [None]
        [final]   0.0000e+00 == gam [rad]
        [path]    1.0000e+02 <= h <= 2.0000e+04  [m]
        [path]    1.0000e-01 <= aero.mach <= 1.8000e+00  [None]

--------------------------------------------------------------------------------
--- Analytic derivatives in component ------------------------------------------
-------------------------------------------------------------------------------- 

Model viewer data has already been recorded for Driver.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/recorders/sqlite_recorder.py:231: UserWarning:The existing case recorder file, /home/runner/work/dymos/dymos/docs/dymos_book/faq/problem_out/dymos_solution.db, is being overwritten.

Model viewer data has already been recorded for Driver.

Full total jacobian for problem 'problem' was computed 3 times, taking 0.2583554529999219 seconds.
Total jacobian shape: (361, 212) 


Jacobian shape: (361, 212)  (3.44% nonzero)
FWD solves: 13   REV solves: 0
Total colors vs. total size: 13 vs 212  (93.87% improvement)

Sparsity computed using tolerance: 1e-12
Time to compute sparsity:   0.2584 sec
Time to compute coloring:   0.1918 sec
Memory to compute coloring:   0.1250 MB
Coloring created on: 2024-11-18 20:36:35

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/total_jac.py:1652: DerivativesWarning:Constraints or objectives [('traj.phases.phase0->path_constraint->h', inds=[(0, 0)]), ('traj.phases.phase0->path_constraint->mach', inds=[(0, 0)])] cannot be impacted by the design variables of the problem.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/utils/coloring.py:1323: OMDeprecationWarning:display is deprecated. Use display_bokeh for rich html displays of coloringor display_txt for a text-based display.

Jacobian shape: (361, 212)  (3.44% nonzero)
FWD solves: 13   REV solves: 0
Total colors vs. total size: 13 vs 212  (93.87% improvement)

Sparsity computed using tolerance: 1e-12
Time to compute sparsity:   0.2584 sec
Time to compute coloring:   0.1918 sec
Memory to compute coloring:   0.1250 MB
Coloring created on: 2024-11-18 20:36:35

--- Constraint Report [traj] ---
    --- phase0 ---
        [final]   2.0000e+04 == h [m]
        [final]   1.0000e+00 == aero.mach [None]
        [final]   0.0000e+00 == gam [rad]
        [path]    1.0000e+02 <= h <= 2.0000e+04  [m]
        [path]    1.0000e-01 <= aero.mach <= 1.8000e+00  [None]

--------------------------------------------------------------------------------
--- Finite differenced component -----------------------------------------------
-------------------------------------------------------------------------------- 

Model viewer data has already been recorded for Driver.
Model viewer data has already been recorded for Driver.

Full total jacobian for problem 'problem2' was computed 3 times, taking 0.2926003299999138 seconds.
Total jacobian shape: (361, 212) 

Jacobian shape: (361, 212)  (23.30% nonzero)
FWD solves: 154   REV solves: 0
Total colors vs. total size: 154 vs 212  (27.36% improvement)

Sparsity computed using tolerance: 1e-12
Time to compute sparsity:   0.2926 sec
Time to compute coloring:   0.9342 sec
Memory to compute coloring:   1.8125 MB
Coloring created on: 2024-11-18 20:36:43

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/total_jac.py:1652: DerivativesWarning:Constraints or objectives [('traj.phases.phase0->path_constraint->h', inds=[(0, 0)]), ('traj.phases.phase0->path_constraint->mach', inds=[(0, 0)])] cannot be impacted by the design variables of the problem.

Jacobian shape: (361, 212)  (23.30% nonzero)
FWD solves: 154   REV solves: 0
Total colors vs. total size: 154 vs 212  (27.36% improvement)

Sparsity computed using tolerance: 1e-12
Time to compute sparsity:   0.2926 sec
Time to compute coloring:   0.9342 sec
Memory to compute coloring:   1.8125 MB
Coloring created on: 2024-11-18 20:36:43

--- Constraint Report [traj] ---
    --- phase0 ---
        [final]   2.0000e+04 == h [m]
        [final]   1.0000e+00 == aero.mach [None]
        [final]   0.0000e+00 == gam [rad]
        [path]    1.0000e+02 <= h <= 2.0000e+04  [m]
        [path]    1.0000e-01 <= aero.mach <= 1.8000e+00  [None]

--------------------------------------------------------------------------------
--- Finite differenced component with partial coloring -------------------------
-------------------------------------------------------------------------------- 

Model viewer data has already been recorded for Driver.
Model viewer data has already been recorded for Driver.

Coloring for 'traj.phases.phase0.rhs_disc.aero.q_comp' (class DynamicPressureCompFD)

Jacobian shape: (60, 120)  (1.67% nonzero)
FWD solves: 2   REV solves: 0
Total colors vs. total size: 2 vs 120  (98.33% improvement)

Sparsity computed using tolerance: 1e-06
Time to compute sparsity:   0.0068 sec
Time to compute coloring:   0.0073 sec
Memory to compute coloring:   0.0000 MB

Coloring for 'traj.phases.phase0.rhs_col.aero.q_comp' (class DynamicPressureCompFD)

Jacobian shape: (30, 60)  (3.33% nonzero)
FWD solves: 2   REV solves: 0
Total colors vs. total size: 2 vs 60  (96.67% improvement)

Sparsity computed using tolerance: 1e-06
Time to compute sparsity:   0.0037 sec
Time to compute coloring:   0.0039 sec
Memory to compute coloring:   0.0000 MB

Full total jacobian for problem 'problem3' was computed 3 times, taking 0.30879589099993154 seconds.
Total jacobian shape: (361, 212) 


Jacobian shape: (361, 212)  (3.44% nonzero)
FWD solves: 13   REV solves: 0
Total colors vs. total size: 13 vs 212  (93.87% improvement)

Sparsity computed using tolerance: 1e-12
Time to compute sparsity:   0.3088 sec
Time to compute coloring:   0.1916 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:37:00

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/total_jac.py:1652: DerivativesWarning:Constraints or objectives [('traj.phases.phase0->path_constraint->h', inds=[(0, 0)]), ('traj.phases.phase0->path_constraint->mach', inds=[(0, 0)])] cannot be impacted by the design variables of the problem.

Jacobian shape: (361, 212)  (3.44% nonzero)
FWD solves: 13   REV solves: 0
Total colors vs. total size: 13 vs 212  (93.87% improvement)

Sparsity computed using tolerance: 1e-12
Time to compute sparsity:   0.3088 sec
Time to compute coloring:   0.1916 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:37:00

<Figure size 550x550 with 0 Axes>

Performance comparison

In this instance, the following performance was noted for the minimum time-to-climb case with 30 Gauss-Lobatto segments. Using OpenMDAO’s partial derivative coloring buys back a signficant amount of performance lost to finite differencing. It should be noted that the IPOPT option alpha_for_y can have a signficant impact on performance here. The default ‘primal’ step results in faster convergence for the sparse analytic case, but results in problematic convergence for the finite-differenced versions. Switching the option using p.driver.opt_settings['alpha_for_y'] = 'safer-min-dual-infeas' results in a ‘safer’ step size and faster convergence of the finite-differenced versions, at the expense of some time in the analytic case. The table below shows approximate run times normalized by the analytic version of the problem’s run time.

Derivative Type	Normalized Optimization Time
Sparse Analytic	1.0
Finite Difference (Dense)	~1.5 to ~2.5
Finite Difference (with Coloring)	~1.0 to ~1.5

Another note is that even in the finite differencing cases only a single component, the dynamic pressure component, is being switch to use finite differencing. Doing so completely destroys the sparsity of the system, requiring over 10x as many solves of the resulting linear system to compute the total derivatives across the model. This is an important lesson: Failing to employ sparsity everywhere in a complex model can completely negate its benefit. However, you can buy back a significant portion of this lost performance using partial coloring.